이제껏 종속 변수 y 값이 연속형인 데이터의 수치를 예측하기 위한 선형 회귀를 알아봤습니다!
하지만 데이터는 다양합니다. 아래 그림처럼 종속 변수 y가 이산형이고, 범주형이라면? '예' or '아니오'로 수치가 아닌 정답을 원하는 데이터라면? 선형 회귀를 적용할 수 없습니다.
로지스틱 회귀는 바로 여기서 출발합니다.
로지스틱 회귀는 참 or 거짓을 판단해 주는 미니 판단 장치인 셈인 것이죠.

그림을 아무리 봐도 선형 회귀선을 그릴 수가 없죠? 직선이 아니라 S자 형태의 함수를 이용해야 합니다.
하지만 우리는 앞에서 S자 형태의 함수를 배운 적이 있습니다. 바로 '시그모이드 함수' 입니다. 로지스틱 회귀는 시그모이드 함수를 이용합니다.




로지스틱 회귀는 이렇게 시그모이드 함수로 표현이 가능합니다. 지수 부분의 x에 ax+b 함수를 대입하면, 그림으로 보듯이 a 값은 그래프의 기울기를 b 값은 함수의 좌우 이동을 의미합니다. 그렇다면 이 미지수들은 또 오차와의 관계를 생각해 볼 수 있죠. 로지스틱 회귀도 똑같이 경사 하강법을 이용하여 오차가 가장 작은 회귀선을 그립니다. 하지만 이전에 단순, 다중 회귀는 MSE의 오차 함수를 이용하지만, 로지스틱 회귀는 로그 함수의 오차 함수를 이용합니다.
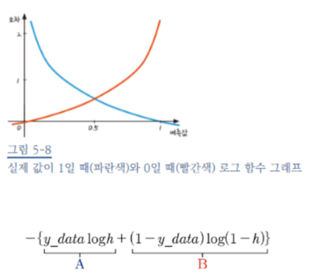
로지스틱 회귀는 옆에 그래프처럼 실제 값이 1일 때는 0으로 예측할 때에 그 오차가 점점 커집니다. 실제 값이 0일 때에는 그 반대죠. 이를 이용해서 오차 함수를 식으로 나타내면 그림 아래의 식을 표현할 수 있어요. 우리는 이제 이 오차 함수식을 이용해서 이전에 연속형 데이터의 회귀처럼 편미분을 통해서 경사 하강법을 실행할 거예요.
<로지스틱 회귀 코딩>


사실은 로지스틱 회귀를 이렇게 코딩 몇 줄로 간단히 했지만, 학교 수업 들었을 적에는 수학적인 원리를 이해하느라 굉장히 애를 먹었던 기억이 나네요. 어려운 원리를 이렇게 쉽게 접근할 수 있다는 점이 이 책의 굉장한 장점인 것 같습니다!
이렇게 5장 로지스틱 회귀도 포스팅 마무리합니다.
'데이터 과학 관련 스터디 > 모두의 딥러닝' 카테고리의 다른 글
| [모두의 딥러닝] 8장 오차 역전파/ 9장 신경망에서 딥러닝으로 (0) | 2020.06.11 |
|---|---|
| [모두의 딥러닝] 6장/7장 단층, 다층 퍼셉트론 (1) | 2020.06.01 |
| [모두의 딥러닝] 4장 오차 수정하기 : 경사 하강법 (0) | 2020.05.10 |
| [모두의 딥러닝] 3장 가장 훌륭한 예측선 긋기 : 선형 회귀 (0) | 2020.04.23 |
| [모두의 딥러닝] 1장, 2장 (0) | 2020.04.14 |




댓글